北中入試 過去問題
問題
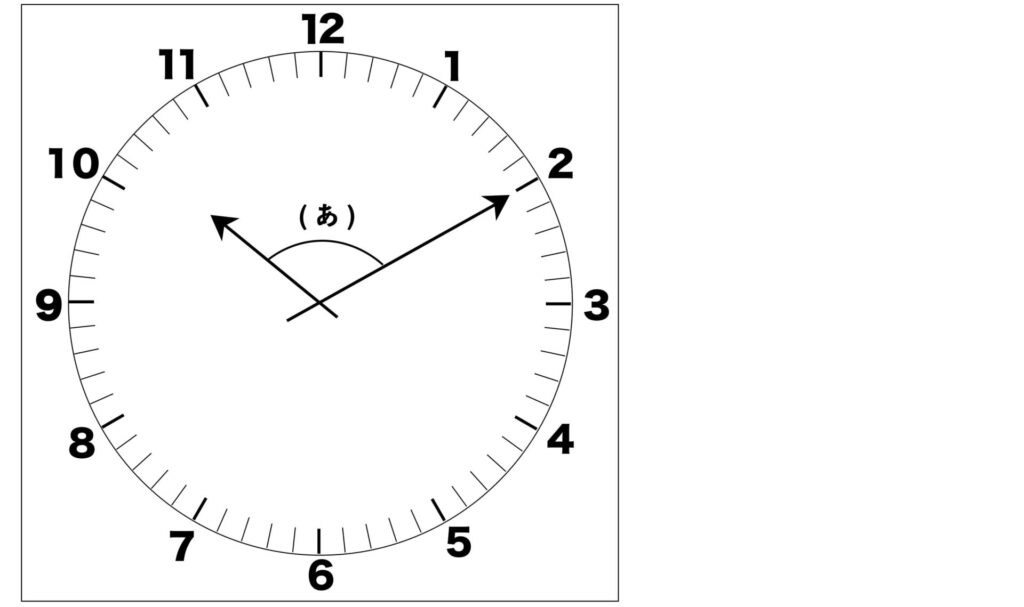
2. 下の図は、10時10分 を示している時計です。あきらさんは、この時間を見て、はじめは長身(ちょうしん)と短針の間の(あ)の角の大きさは120° であると考えましたが、短針が文字ばんの 10 の位置からずれていることに気づき、(あ)の角の大きさは120° ではないことが分かりました。(あ)の角の大きさは何度ですか。また、その求め方も書きなさい。
じっくり考えてみましょう。
解答
角の大きさ: 115度
求め方①:
360°÷3=120°だから、右の図の角の大きさは120°である。
短針は、12時間で360°進む。
360°÷12=30° だから1時間で30°進み、
30°÷60=0.5° だから1分で0.5°進む。
短針は10の位置から10分進んでいるので、0.5°×10=5°
これより、120°-5°=115° だから、(あ)の角の大きさは115°である。
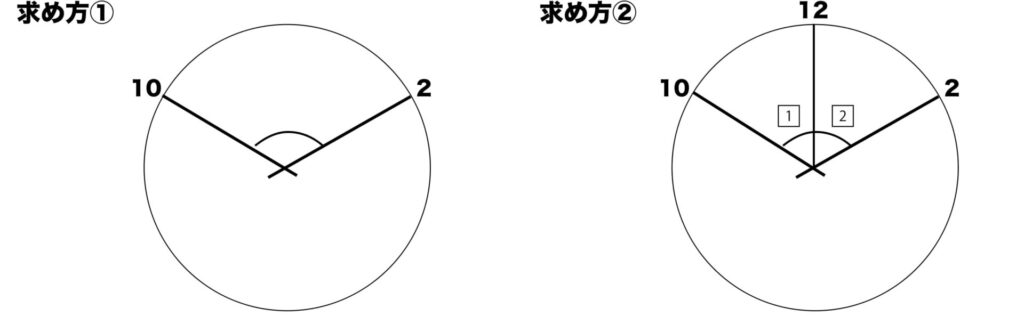
求め方②:
短針は12時間で360°進むので、2時間で60°進む。
だから、①の角の大きさは60°である。
長針は60分で360°進むので、10分で60°進む。
だから②の角の大きさは60°である。短針は10の位置から10分進んでいるので、30°÷6=5°で、5°進んでいる。
60°+60°-5°=115°だから、(あ)の角の大きさは115°である。
皆さん、答えられたかな?それでは解説を見てみましょう。
解説
求め方①は、10の位置から2の位置までの角度を求め、そこから短針が進んだ分を引く方法です。
求め方②は、12の位置を基準として10の位置から12の位置まで、12の位置から長針までの角度を求め、その合計から10の位置から短針までの角度を引く方法です。
どちらの求め方でも、重要なのは10の位置と短針が何度離れているのか、ということ。
・短針は12時間で360°進む
・1時間では360°÷12=30°
・10分では30°÷6=5°(1時間は60分)
・1分では30°÷60=0.5°
を正しく理解できたか、確認しておこう。
円の中心角は360°です。時計も円形なので中心角は360°である、と考えられますよね!
↓この問題の解説動画を見る↓











