北中入試 過去問題
問題
1. 下の図のように、厚紙でつくった立方体を太線で示した辺にそって切り開いて展開図をつくります。
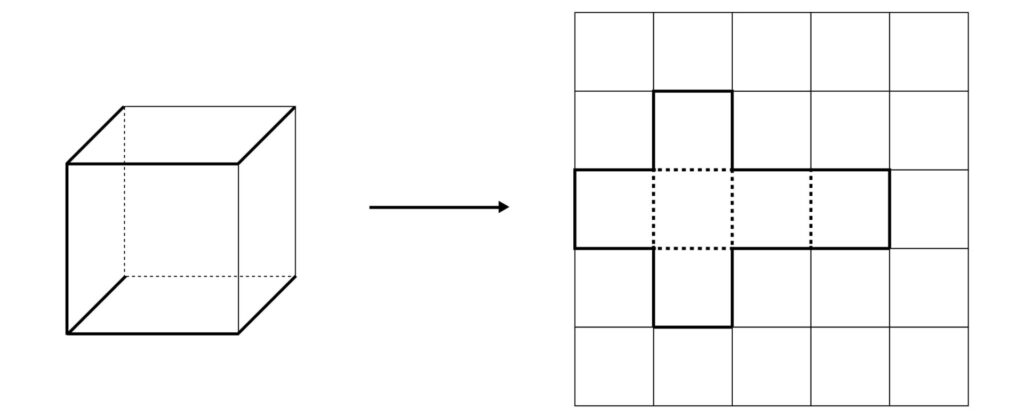
立方体を切り開いて展開図をつくるには、立方体のどの辺にそって切り開けばよいですか。できる展開図が合同ではないものを上の図以外に２つ考え、解答用紙の立方体の図に切り開く辺を太線で示しなさい。また、そのときにできる展開図をかきなさい。
少し難しい問題ですね。じっくり考えてみましょう。
解答
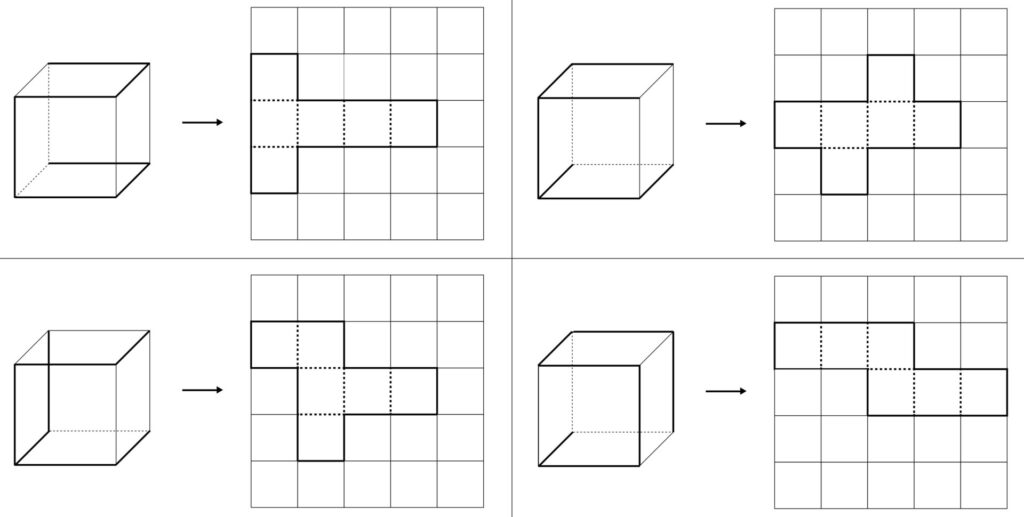
などから２つ
皆さん、答えられたかな？それでは解説を見てみましょう。
解説
先に展開図を考えて、次にその時に切り開く辺を太線にすると分かりやすいですよ。
例えば、問題の展開図のつかい、Aはふた、Fは底、B〜Eは側面と考えます。
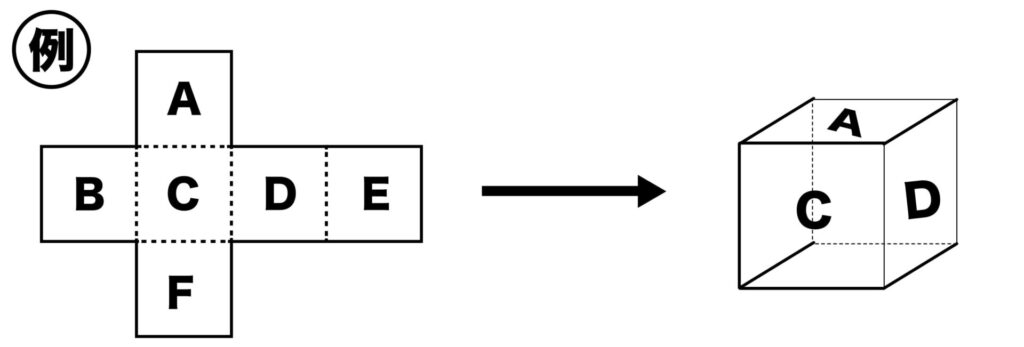
まず、上の例と同じように、Aはふた、Fは底、B〜Eは側面の展開図を考えます。
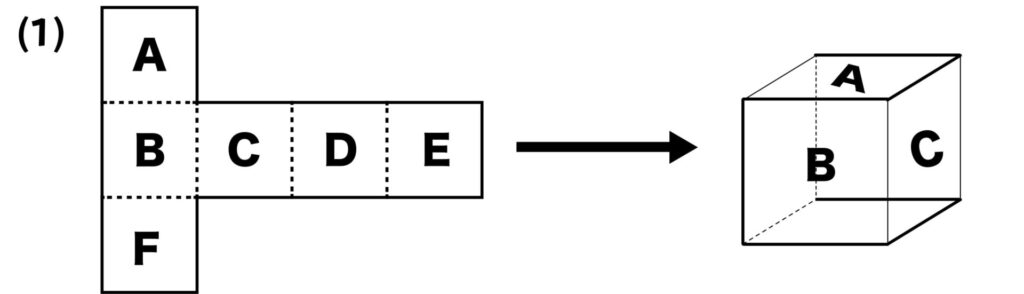
合同（同じ形）ではないものを考えなければならないので、下の形は答えになりません。
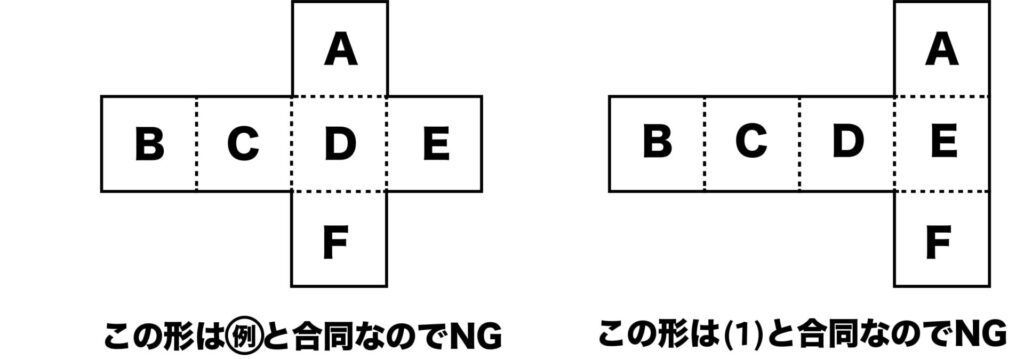
ふたと底は展開図の同じ面についてなくても良いので、下記の図が考えられます。
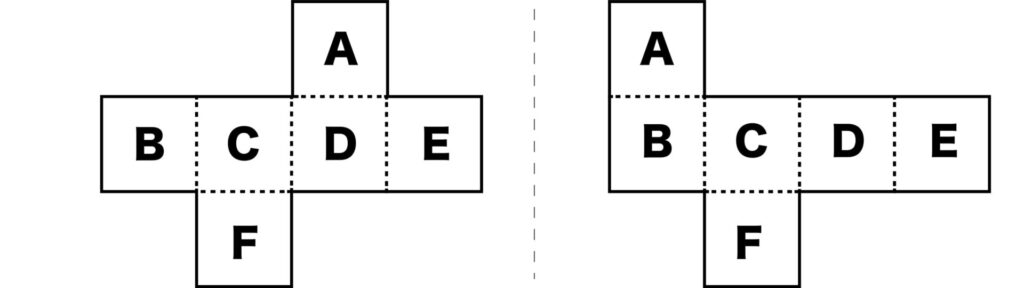
また、例の展開図の変形としてBの位置を動かした下記の図も考えられます。
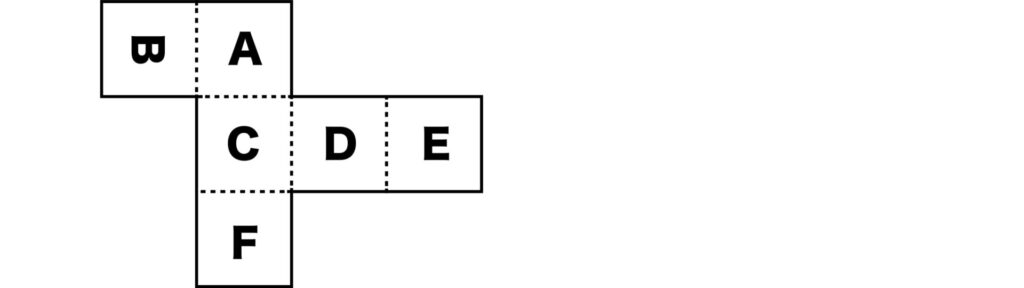
さらに、Fの位置を変えた下記の図も考えられます。
ベースの形から少しずつ動かして考えてみよう！
↓この問題の解説動画を見る↓
