北中入試 過去問題
問題
2.会議室にある長方形のテーブルは、下の図1のように、長い辺には3人、短い辺には2人座ることができます。会議を行うとき、参加人数が増えると、このテーブルを図2のように長い辺どうしをあわせたり、短いへんどうしをあわせたりして、参加者はテーブルの周りに座ります。これについて、次の問いに答えなさい。

(2)何台かのテーブルを長い辺どうしをあわせて1列に並べ、その周りに座ってみたところ、12人の参加者が座れなくなりました。そこで、テーブルの台数を変えずに、短い辺どうしをあわせて1列に並べると、空席ができることなく参加者全員が座ることができました。長方形のテーブルを何台並べたか、その台数を書きなさい。また、その求め方も書きなさい。
じっくり考えて答えましょう。
解答
テーブルの数:7台
求め方:
例①

座れる人数のちがいが12人になるのは、テーブルを7台並べたときである。
例②
テーブルを2台どうし並べるとき、長い辺どうしを合わせたときは14人、短い辺どうしを合わせたときは16人座ることができる。この時、座ることのできる人数の違いは2人である。
12人が座れないから、12÷2=6より、テーブルを合わせた部分は6か所である。
よって、テーブルの台数は、6+1=7より、7台である。
などから1つ
皆さん、答えられたかな?それでは解説を見てみましょう。
解説
解答例①は表の通りなので、解答例②を解説します。
まずは、テーブル2台を並べてみます。
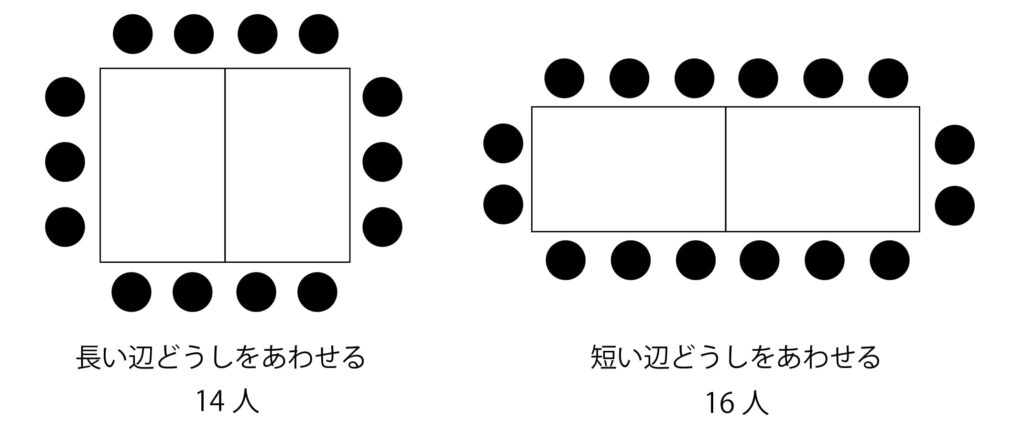
長い辺どうしあわせた人数と短い辺どうしあわせた人数の差は16−14=2より、2人です。
求めているのは12人座れなかった場合なので、12÷2=6
この6というのは、テーブルをつなぎあわせた部分です。

6か所テーブルをつなぎあわせた部分があるので、全体のテーブルの数は6+1=7より、7テーブルである。
図を書いてみると分かりやすいですね。










-1-640x360.jpg)


